Simulating and Modeling Statistical Distributions via bayes.js
Published:
I have been thinking about building a web app for simulating data with given parameters and recovering the parameters with Bayesian MCMC samplers in JavaScript. This web app can not only make the procedures more transparent, but also help us understand the magic of the Bayesian MCMC approach. More importantly, I have benefited from this simulation-based way of thinking, so I would like to promote it in my blog.

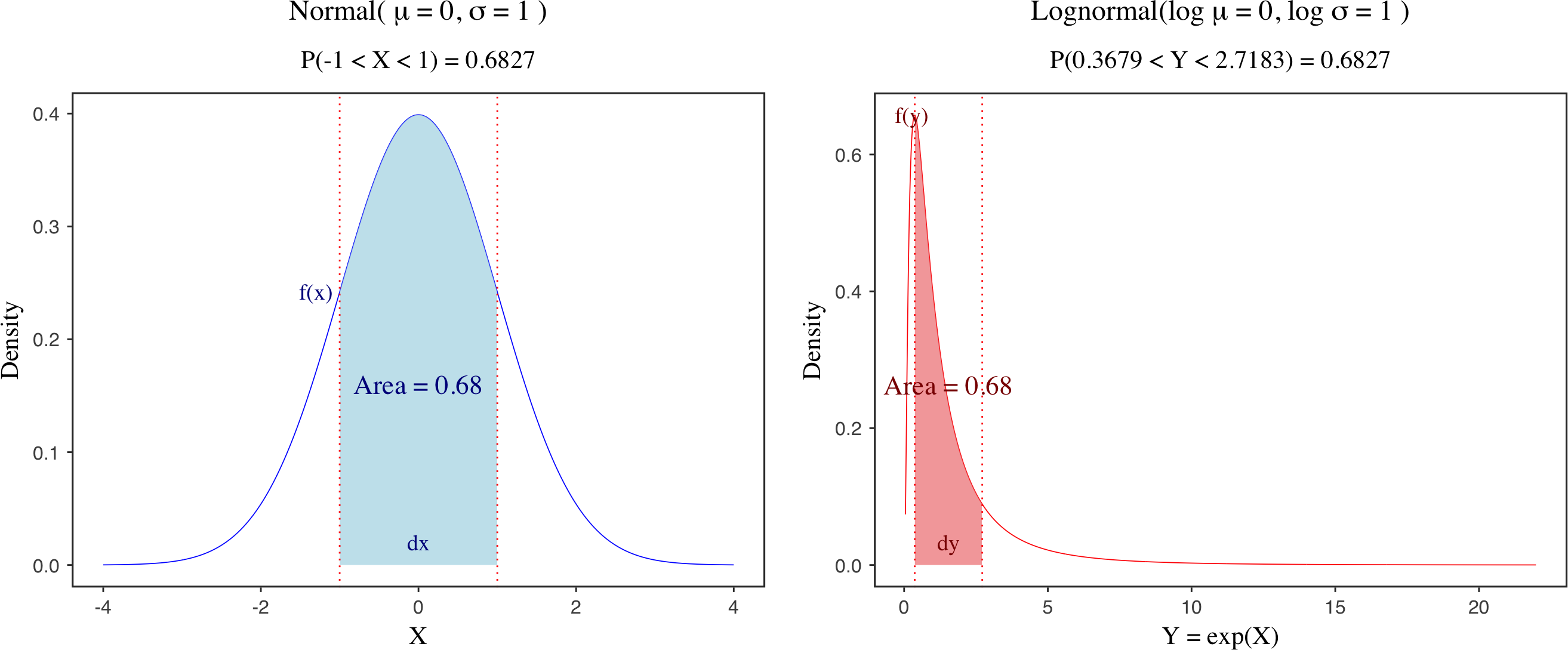
)](https://raw.githubusercontent.com/JakeJing/jakejing.github.io/master/_posts/pics/multi-logistic-reg-surface.png)
)](https://raw.githubusercontent.com/JakeJing/jakejing.github.io/master/_posts/pics/nest_split.png)